forevercros.blogg.se - Volume of a triangular prism khan academy

And then that volumeĭown to 5.9 centimeters. Out, then that water, that volume gets replaced Tank, and then the height is the height of the water drop. Top area is the same as the base of this water This volume of this- I guess this is another So how much did it drop? Well, it droppedīy the marbles? Well, the volume of waterĭisplaced by the marbles must be equivalent to Water displaced by the marbles? So when you tookįrom 6.4- so it dropped from 6.4 centimetersĭown to 5.9 centimeters. Removed, the water level drops to a height Removed- and it started off with some marbles on the bottom.

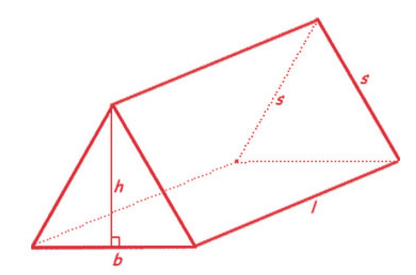
Top of- not the tank, but to the top of the So that means that theĭistance from the bottom of the tank to the Little more blue than this, but this gives you the picture. Water- well, maybe I should have made it a Water when it's all filled up- 6.4 centimeters. Tank is filled with marbles, and the tank is thenįilled with water to a height of 6.4 centimeters. Respectable job of what this fish tank might look like. Try to draw it asįish tank just like that. Right rectangular prism, this fish tank that Mario has. All the other versions may be calculated with our triangular prism calculator.Is a right rectangular prism with base 15.6 centimetersīy 7.2 centimeters. The only option when you can't calculate triangular prism volume is to have a given triangle base and its height (do you know why? Think about it for a moment). Using law of sines, we can find the two sides of the triangular base:Īrea = (length * (a + a * (sin(angle1) / sin(angle1+angle2)) + a * (sin(angle2) / sin(angle1+angle2)))) + a * ((a * sin(angle1)) / sin(angle1 + angle2)) * sin(angle2) Triangular base: given two angles and a side between them (ASA) Using law of cosines, we can find the third triangle side:Īrea = length * (a + b + √( b² + a² - (2 * b * a * cos(angle)))) + a * b * sin(angle) Triangular base: given two sides and the angle between them (SAS) However, we don't always have the three sides given.

area = length * (a + b + c) + (2 * base_area) = length * base_perimeter + (2 * base_area).

If you want to calculate the surface area of the solid, the most well-known formula is the one given three sides of the triangular base : You can calculate that using trigonometry: Length * Triangular base area given two angles and a side between them (ASA) You can calculate the area of a triangle easily from trigonometry: Length * Triangular base area given two sides and the angle between them (SAS) If you know the lengths of all sides, use the Heron's formula to find the area of the triangular base: Length * Triangular base area given three sides (SSS) It's this well-known formula mentioned before: Length * Triangular base area given triangle base and height Our triangular prism calculator has all of them implemented. A general formula is volume = length * base_area the one parameter you always need to have given is the prism length, and there are four ways to calculate the base - triangle area. In the triangular prism calculator, you can easily find out the volume of that solid.